Hai đường thẳng song song là một chủ đề quan trọng trong chương trình Toán lớp 7. Hiểu rõ về khái niệm, tính chất và dấu hiệu nhận biết của hai đường thẳng song song sẽ giúp học sinh giải quyết các bài toán liên quan một cách dễ dàng.
Định nghĩa hai đường thẳng song song
Hai đường thẳng được gọi là song song (kí hiệu: //) nếu chúng không có điểm chung nào.
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Kí hiệu: a // b
Tính chất hai đường thẳng song song
Tính chất 1: Hai đường thẳng song song thì các cặp góc so le trong bằng nhau.
Cho hai đường thẳng a // b và đường thẳng c cắt a, b lần lượt tại A và B.
Ta có:
∠A1 và ∠B2 là hai góc so le trong.
∠A1 = ∠B2 (tính chất hai đường thẳng song song)
Tính chất 2: Hai đường thẳng song song thì các cặp góc đồng vị bằng nhau.
Cho hai đường thẳng a // b và đường thẳng c cắt a, b lần lượt tại A và B.
Ta có:
∠A1 và ∠C1 là hai góc đồng vị.
∠A1 = ∠C1 (tính chất hai đường thẳng song song)
Tính chất 3: Hai đường thẳng song song thì các cặp góc trong cùng phía bù nhau.
Cho hai đường thẳng a // b và đường thẳng c cắt a, b lần lượt tại A và B.
Ta có:
∠A1 và ∠B1 là hai góc trong cùng phía.
∠A1 + ∠B1 = 180° (tính chất hai đường thẳng song song)
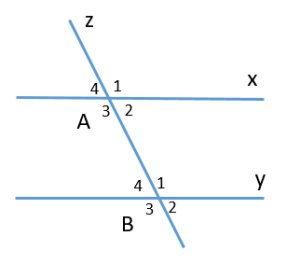
Dấu hiệu nhận biết hai đường thẳng song song
Dấu hiệu 1: Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.
Dấu hiệu 2: Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
Dấu hiệu 3: Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau thì hai đường thẳng song song.
Các dạng toán thường gặp bài hai đường thẳng song song
Dạng 1: Chứng minh hai đường thẳng song song dựa vào
Tính chất:
Hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau.
Hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau.
Hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau.
Dấu hiệu nhận biết:
Hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau.
Hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau.
Hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc trong cùng phía bù nhau.
Ví dụ:
Bài tập: Cho hai đường thẳng a và b cắt nhau tại O. Vẽ đường thẳng c sao cho ∠aOc = ∠bOc. Chứng minh rằng a // b.
Giải:
Vì ∠aOc = ∠bOc nên a // b (theo dấu hiệu nhận biết hai đường thẳng song song)
Dạng 2: Vận dụng tính chất của hai đường thẳng song song để giải bài toán.
Ví dụ:
Bài tập: Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c cắt a, b lần lượt tại A và B. Chứng minh rằng:
∠A1 = ∠B2.
∠A2 = ∠B1.
Giải:
Chứng minh ∠A1 = ∠B2:
Vì a // b và c cắt a, b lần lượt tại A và B nên:
∠A1 và ∠B2 là hai góc so le trong.
Suy ra: ∠A1 = ∠B2 (tính chất hai đường thẳng song song)
Chứng minh ∠A2 = ∠B1:
Vì a // b và c cắt a, b lần lượt tại A và B nên:
∠A2 và ∠B1 là hai góc đồng vị.
Suy ra: ∠A2 = ∠B1 (tính chất hai đường thẳng song song)
Dạng 3: Tìm số đo các góc trong hình vẽ.
Vẽ hình minh họa để bài giải được rõ ràng và dễ hiểu.
Bài tập:
Bài tập 1: Cho hai đường thẳng m và n cắt nhau tại O. Một đường thẳng p vuông góc với đường thẳng m tại A. Một đường thẳng q vuông góc với đường thẳng n tại B. Chứng minh rằng p // q.
Bài tập 2: Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c cắt a, b lần lượt tại A và B. Tính số đo các góc ∠A1, ∠A2, ∠B1, ∠B2 biết ∠A1 = 40°.
Bài tập có lời giải chi tiết cho bài hai đường thẳng song song
Bài tập 1: Cho hai đường thẳng a và b cắt nhau tại O. Vẽ đường thẳng c sao cho ∠aOc = ∠bOc. Chứng minh rằng a // b.
Giải:
Cách 1:
Vì ∠aOc = ∠bOc nên Oz là tia phân giác của góc ∠aOb.
Do đó, Oz nằm giữa hai tia Oa và Ob.
Ta có:
∠aOz + ∠bOz = ∠aOb = 180° (kề bù)
∠aOz = ∠bOz (vì Oz là tia phân giác của góc ∠aOb)
Suy ra: ∠aOz = ∠bOz = 90°
Lại có:
∠aOz và ∠bOz là hai góc so le trong
Do đó, a // b (theo dấu hiệu nhận biết hai đường thẳng song song)
Cách 2:
Vì ∠aOc = ∠bOc nên a // c (theo dấu hiệu nhận biết hai đường thẳng song song)
Lại có:
a // c và b cắt a, c lần lượt tại A và C
Suy ra: b // a (theo tính chất hai đường thẳng song song)
Bài tập 2: Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c cắt a, b lần lượt tại A và B. Tính số đo các góc ∠A1, ∠A2, ∠B1, ∠B2 biết ∠A1 = 40°.
Giải:
Vì a // b và ∠A1 = 40° nên:
∠B1 = ∠A1 = 40° (tính chất hai đường thẳng song song)
∠A2 + ∠B1 = 180° (tính chất hai góc trong cùng phía)
Suy ra: ∠A2 = 180° – ∠B1 = 180° – 40° = 140°
∠B2 = ∠A2 = 140° (tính chất hai đường thẳng song song)
Bài tập 3: a // b và ∠C1 = 120°. Tính số đo các góc ∠A1, ∠A2, ∠B1, ∠B2.
Giải:
Vì a // b và ∠C1 = 120° nên:
∠B1 = ∠C1 = 120° (tính chất hai đường thẳng song song)
∠A1 + ∠B1 = 180° (tính chất hai góc trong cùng phía)
Suy ra: ∠A1 = 180° – ∠B1 = 180° – 120° = 60°
∠B2 = ∠A1 = 60° (tính chất hai đường thẳng song song)
∠A2 + ∠C1 = 180° (tính chất hai góc trong cùng phía)
Suy ra: ∠A2 = 180° – ∠C1 = 180° – 120° = 60°
Hai đường thẳng song song là một chủ đề cơ bản nhưng rất quan trọng trong chương trình Toán lớp 7. Nắm vững kiến thức về chủ đề này sẽ giúp học sinh giải quyết các bài toán liên quan một cách dễ dàng và hiệu quả.








