Định lý Py-ta-go là một trong những định lí quan trọng nhất trong môn Toán học lớp 7. Nó được xem là nền tảng cho nhiều kiến thức toán học sau này, đặc biệt là trong chương Hình học.
Định lí Py-ta-go
Định lí Py-ta-go là một trong những định lí quan trọng nhất trong môn Toán học. Định lí này liên hệ giữa độ dài các cạnh của một tam giác vuông.
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.
Công thức:
c² = a² + b²
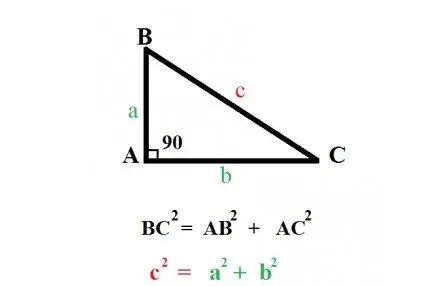
Với:
c là độ dài cạnh huyền
a và b là độ dài hai cạnh góc vuông
Định lý Py-ta-go đảo
Định lý Py-ta-go đảo phát biểu như sau: “Trong một tam giác bất kỳ, bình phương của một cạnh bằng tổng bình phương của hai cạnh còn lại, thì góc giữa hai cạnh này bằng 90 độ“.
Công thức của định lý Py-ta-go đảo như sau:
c² = a² + b²
Trong đó:
c là cạnh huyền của tam giác
a và b là hai cạnh kề của tam giác
Ngược lại với định lý Py-ta-go thuận, người ta cùng định lý Pytago đảo để chứng minh tam giác vuông khi biết chiều dài các cạnh của tam giác đó.
Ứng dụng của định lý Py-ta-go
Định lí Py-ta-go có nhiều ứng dụng trong thực tế, ví dụ như:
Tính độ dài cạnh của tam giác vuông
Chứng minh tam giác vuông
Giải các bài toán liên quan đến hình vuông, hình chữ nhật, hình thoi, v.v.
Chứng minh định lí Py-ta-go
Có nhiều cách để chứng minh định lí Py-ta-go, bạn có thể tham khảo một số cách chứng minh phổ biến sau:
Chứng minh bằng cách diện tích
Chia tam giác vuông ABC thành hai tam giác vuông AHB và AHC.
Chứng minh diện tích tam giác ABC bằng tổng diện tích hai tam giác vuông AHB và AHC.
Từ đó, suy ra định lí Py-ta-go.
Chứng minh bằng cách vectơ
Sử dụng vectơ để biểu diễn các cạnh của tam giác vuông ABC.
Chứng minh công thức vectơ cho bình phương độ dài của một vectơ.
Từ đó, suy ra định lí Py-ta-go.
Bài tập vận dụng định lí Py-ta-go
Bài 1: Cho tam giác ABC vuông tại A, biết AB = 3cm, AC = 4cm. Tính BC.
Lời giải:
Áp dụng định lí Py-ta-go, ta có:
BC² = AB² + AC² = 3² + 4² = 9 + 16 = 25
BC = √25 = 5cm
Vậy BC = 5cm.
Bài 2: Cho tam giác ABC vuông tại A, biết BC = 10cm, AB = 6cm. Tính AC.
Lời giải:
Áp dụng định lí Py-ta-go, ta có:
AC² = BC² – AB² = 10² – 6² = 100 – 36 = 64
AC = √64 = 8cm
Vậy AC = 8cm.
Bài 3: Cho tam giác ABC vuông tại A, biết AC = 8cm, BC = 10cm. Tính AB.
Lời giải:
Áp dụng định lí Py-ta-go, ta có:
AB² = BC² – AC² = 10² – 8² = 100 – 64 = 36
AB = √36 = 6cm
Vậy AB = 6cm.
Bài 4: Cho tam giác ABC vuông tại A, biết AB = 4cm, AC = 3cm. Tính BC.
Lời giải:
Áp dụng định lí Py-ta-go, ta có:
BC² = AB² + AC² = 4² + 3² = 16 + 9 = 25
BC = √25 = 5cm
Vậy BC = 5cm.
Bài 5:
Cho tam giác ABC vuông tại A, biết BC = 8cm, AC = 6cm. Tính AB.
Lời giải:
Áp dụng định lí Py-ta-go, ta có:
AB² = BC² – AC² = 8² – 6² = 64 – 36 = 28
AB = √28 ≈ 5,29cm
Vậy AB ≈ 5,29cm.
Luyện tập
Bài 1:
Cho DABC vuông tại A. biết AB + AC = 49cm; AB – AC = 7cm. Tính cạnh BC.
Bài 2:
Cho DABC vuông tại A. có BC = 26cm, AB:AC = 5:12. Tính độ dài AB và AC.
Bài 3:
Cho DABC vuông tại A. Kẻ đ ường cao AH. Biết BH = 18 cm; CH = 32cm. Tính các cạnh AB và AC.
Bài 4:
Cho DABC có AB = 9cm; AC = 11cm. Kẻ đường cao AH, bi ết BH = 26cm. Tính CH ?
Bài 5: Cho DABC vuông tại A. Kẻ AH vuông góc BC.
a/ Chứng minh: AB2 + CH2 = AC2 + BH2
b/ Trên AB lấy E, trên AC lấy đi ểm F. Ch ứng minh: EF < BC.
c/ Bi ết AB = 6cm, AC = 8 cm. Tính AH, BH, CH.
Bài 6:
Cho DABC cân, AB = AC = 17cm. Kẻ BD vuông góc AC. Tính BC, biết BD = 15cm.
Bài 7: Cho DABC. Biết BC = 52cm, AB = 20cm, AC = 48cm.
a/ CM: DABC vuông ở A.
b/ Kẻ AH vuông góc BC. Tính AH.
Bài 8:
Hãy kiểm tra xem tam giác ABC có phải là tam giác vuông không nếu các cạnh AB, AC và BC tỉ lệ với:
a/ 9; 12 và 15
b/ 3; 2,4 và 1,8.
c/ 4; 6 và 7
d/ 4; 4 và 4.
Bài 9: Cho DABC vuông tại A, đường cao AH, trên đó lấy điểm D. Trên tia đối của tia HA lấy E sao cho HE = AD. Đường vuông góc với AH tại D cắt AC tại F.
Chứng minh rằng: EB vuông góc EF.
Bài 10: Cho góc nhọn xOy. Điểm H nằm trên tia phân giác của góc xOy. Từ H dựng các đường vuông góc xuống hai cạnh Ox và Oy (A thuộc Ox và B thuộc Oy).
a) Chứng minh tam giác HAB là tam giác cân
b) Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH.
Chứng minh BC ⊥ Ox.
c) Khi góc xOy bằng 600, chứng minh OA = 2OD.
Tóm lại, Định lí Py-ta-go là một định lí quan trọng trong môn Toán học lớp 7. Nó có nhiều tính chất và ứng dụng trong thực tế. Việc nắm vững kiến thức về Định lí Py-ta-go là rất cần thiết để giải các bài toán liên quan.
