Bạn đang học Toán lớp 10 và muốn chinh phục chủ đề “Cung và góc lượng giác”? Bài viết này sẽ là cẩm nang hữu ích giúp bạn khám phá thế giới đầy thú vị của cung và góc lượng giác, từ định nghĩa cơ bản đến ứng dụng thực tiễn trong cuộc sống.
Định nghĩa cung và góc lượng giác
Cung lượng giác
- Là một phần của đường tròn giới hạn bởi hai đầu mút là hai điểm A và B trên đường tròn.
- Ký hiệu: ∠(A,B) hoặc ⁀AB.
- Cung nhỏ: Cung có độ dài nhỏ hơn nửa đường tròn.
- Cung lớn: Cung có độ dài lớn hơn hoặc bằng nửa đường tròn.
Góc lượng giác
- Là góc có đỉnh O là tâm đường tròn và hai cạnh OA và OB là hai tia tạo thành cung lượng giác.
- Góc lượng giác có số đo dương: Góc quay ngược chiều kim đồng hồ.
- Góc lượng giác có số đo âm: Góc quay theo chiều kim đồng hồ.
Đơn vị đo cung và góc lượng giác
Độ: Là đơn vị đo phổ biến nhất của cung và góc lượng giác.
- Ký hiệu: °.
- Một vòng tròn đầy đủ có số đo là 360°.
Radian:Là đơn vị đo tự nhiên của cung và góc lượng giác.
- Ký hiệu: rad.
- Cung có độ dài bằng bán kính đường tròn chứa cung ấy có số đo là 1 rad.
Quy đổi giữa độ và radian
- 1° = π/180 rad
- 1 rad = 180°/π
Ví dụ
- Cung AB có số đo 60° có số đo bằng π/3 rad.
- Góc lượng giác (OA, OB) có số đo 45° có số đo bằng π/4 rad.
Ưu điểm và nhược điểm của từng đơn vị
Độ:
- Ưu điểm: Dễ sử dụng, dễ hình dung.
- Nhược điểm: Không phải là đơn vị tự nhiên, không thuận tiện cho việc tính toán.
Radian:
- Ưu điểm: Là đơn vị tự nhiên, thuận tiện cho việc tính toán.
- Nhược điểm: Khó hình dung hơn so với độ.
Mối liên hệ giữa độ và radian
- 1 rad = 180°/π ≈ 57,296°.
- 1° ≈ 0,01745 rad.
Giá trị lượng giác của cung lượng giác
- Sin α: Tỉ số giữa tung độ y của điểm M và bán kính R của đường tròn.
- Cos α: Tỉ số giữa hoành độ x của điểm M và bán kính R của đường tròn.
- Tan α: Tỉ số giữa sin α và cos α.
- Cot α: Tỉ số giữa cos α và sin α.
Công thức lượng giác
- Công thức cộng:
- \(sin(α + β) = sin α cos β + cos α sin β\)\(\)
- \(\)cos(α + β) = cos α cos β – sin α sin β\(\)
- \(\)tan(α + β) = (tan α + tan β)/(1 – tan α tan β)\(\)
- Công thức nhân đôi:
- \(\)sin 2α = 2 sin α cos α\(\)
- \(\)cos 2α = cos^2 α – sin^2 α = 1 – 2 sin^2 α = 2 cos^2 α – 1\(\)
- \(\)tan 2α = (2 tan α)/(1 – tan^2 α)\(\)
Ví dụ
- Cho cung ∠(A,B) có số đo α = 60°.
- \(\)Sin α = y/R = √3/2.\(\)
- \(\)Cos α = x/R = 1/2.\(\)
- \(\)Tan α = sin α/cos α = √3.\(\)
- \(\)Cot α = cos α/sin α = 1/√3.\(\)
- Cho tam giác ABC vuông tại A, với AB = 3 cm, AC = 4 cm.
- \(\)Sin B = AC/BC = 4/5.\(\)
- \(\)Cos B = AB/BC = 3/5.\(\)
- \(\)Tan B = AC/AB = 4/3.\(\)
- \(\)Cot B = AB/AC = 3/4.\(\)
Giá trị lượng giác của các góc đặc biệt
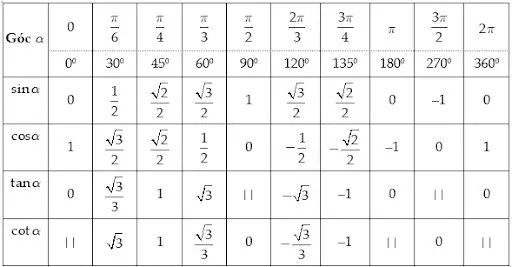
Bài tập có lời giải bài cung và góc lượng giác lớp 10:
Bài 1:
Cho đường tròn tâm O bán kính R = 5cm.
- a) Tìm số đo của cung AB có độ dài s = 3π cm.
- b) Tìm độ dài cung CD có số đo α = 120°.
Lời giải:
a)
Số đo của cung AB được tính theo công thức:
α = s * 360°/2πr
Thay s = 3π cm, r = 5cm, ta được:
α = 3π * 360°/2π * 5 = 108°
b)
Độ dài cung CD được tính theo công thức:
s = α/360° * 2πr
Thay α = 120°, r = 5cm, ta được:
s = 120°/360° * 2π * 5 = 10π cm
Bài 2:
Cho góc α có Sin(α) = 0,8 và Cos(α) = 0,6.
- a) Tính Tan(α) và Cot(α).
- b) Tính số đo của góc α.
Lời giải:
a)
- Tan(α) = Sin(α)/Cos(α) = 0,8/0,6 = 4/3
- Cot(α) = 1/Tan(α) = 3/4
b)
Sử dụng máy tính hoặc bảng lượng giác, ta tìm được:
α ≈ 36,87°
Bài 3:
Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm.
- a) Tính sinα, cosα, tanα, cotα.
- b) Tính số đo góc B, góc C.
Lời giải:
a)
- Sinα = AC/BC = 8/10 = 4/5
- Cosα = AB/BC = 6/10 = 3/5
- Tanα = Sinα/Cosα = 4/3
- Cotα = 1/Tanα = 3/4
b)
- SinB = Cosα = 3/5
- CosB = Sinα = 4/5
Sử dụng máy tính hoặc bảng lượng giác, ta tìm được:
- B ≈ 53,13°
- C = 90° – B ≈ 36,87°
Bài 4:
Một chiếc đồng hồ có kim giờ dài 3cm, kim phút dài 4cm.
- a) Tính tốc độ dài của đầu kim giờ và đầu kim phút.
- b) Vào lúc 6 giờ, hai kim đồng hồ tạo với nhau một góc bao nhiêu độ?
Lời giải:
a)
- Tốc độ dài của đầu kim giờ:
\(\)v_h = ω * R = 2π/12h * 3cm ≈ 0,157 cm/s
- Tốc độ dài của đầu kim phút:
\(\)v_m = ω * R = 2π/60m * 4cm ≈ 0,424 cm/s
b)
Vào lúc 6 giờ, hai kim đồng hồ trùng nhau.
Sau mỗi phút, kim phút quay được 6°, kim giờ quay được 0,5°.
Sau 12h, kim phút quay được 720°, kim giờ quay được 60°.
Góc giữa hai kim đồng hồ lúc này là:
α = 720° – 60° = 660°
Bài tập luyện tập về cung và góc lượng giác lớp 10:
Bài 1. Chọn câu đúng:
Cung có số đo 180° là cung lớn. B. Góc có số đo 180° là góc lượng giác. C. Sinα = y/r. D. Cosα = x/r.
Bài 2. Cho đường tròn tâm O bán kính R = 5cm.
a) Tìm số đo của cung AB có độ dài s = 2π cm. b) Tìm độ dài cung CD có số đo α = 150°.
Bài 3. Cho góc α có Sin(α) = 0,5 và Cos(α) = 0,8.
a) Tính Tan(α) và Cot(α). b) Tính số đo của góc α.
Bài 4. Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm.
a) Tính sinα, cosα, tanα, cotα. b) Tính số đo góc B, góc C.
Bài 5. Một chiếc đồng hồ có kim giờ dài 3cm, kim phút dài 4cm.
a) Tính tốc độ dài của đầu kim giờ và đầu kim phút. b) Vào lúc 3 giờ, hai kim đồng hồ tạo với nhau một góc bao nhiêu độ?
Bài 6. Chứng minh các đẳng thức lượng giác:
a) Sin^2(α) + Cos^2(α) = 1. b) Tan(α) = Sin(α)/Cos(α). c) Cot(α) = 1/Tan(α).
Bài 7. Giải phương trình lượng giác:
a) Sin(x) = 0,5. b) Cos(x) = -0,8.
Bài 8. Bài toán ứng dụng:
Một chiếc quạt trần có cánh dài 1m. Khi quay, cánh quạt tạo với trần nhà một góc 30°. Tính tốc độ dài của đầu cánh quạt.
Hy vọng bài viết này đã cung cấp cho bạn kiến thức nền tảng vững chắc để tiếp tục học tập và ứng dụng vào thực tiễn. Hãy nhớ rằng, luyện tập thường xuyên là chìa khóa để thành thạo chủ đề này.
