Công thức Logarit đóng vai trò quan trọng trong toán học và khoa học. Nó được sử dụng để mô tả các hiện tượng tăng trưởng theo cấp số nhân, ví dụ như sự phân rã phóng xạ hay sự phát triển của vi khuẩn. Trong chương trình Toán lớp 12, học sinh được giới thiệu về các khái niệm cơ bản và công thức liên quan đến hàm số logarit.
Bảng công thức logarit đầy đủ
Với \(x,y > 0\)
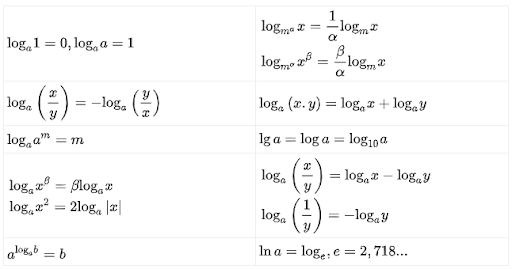
Bảng công thức đạo hàm Logarit

Bảng công thức mũ Logarit

Các dạng bài tập Logarit cơ bản và cách giải
Phương pháp đưa về cùng cơ số
Sử dụng công thức đổi cơ số: \(\log_a x = \frac{\log_b x}{\log_b a}\)
Chọn cơ số thích hợp để việc đổi cơ số trở nên đơn giản.
Bài tập áp dụng
Bài 1: Giải phương trình: \(\log_2 x + \log_3 x = 1\)
Lời giải:
Đưa về cùng cơ số 2:
\(\log_2 x + \frac{\log_2 x}{\log_2 3}= 1\)Giải phương trình:
\(\log_2 x(1+ \frac{1}{log_2 3}) = 1\) \(\log_2 x = \frac{\log_2 3}{\log_2 3+ 1}= 1\) \(x = 2^{\frac{\log_2 3}{\log_2 3 + 1}}\)Bài 2: So sánh: \(\log_5 2\) và \(\log_3 7\)
Lời giải:
Đưa về cùng cơ số 2:
\(\log_5 2=\frac{\log_2 2}{log_2 5}\) và \(\log_3 7= \frac{\log_2 7}{\log_2 3}\)
So sánh
\(\frac{\log_2 2}{\log_2 5} > \frac{\log_2 7}{\log_2 3}\) \(\log_5 2 > \log_3 7\)Phương pháp đặt ẩn phụ
Phương pháp:
Bước 1: Xác định ẩn phụ phù hợp:
- Chọn ẩn phụ là biểu thức xuất hiện nhiều lần hoặc phức tạp trong phương trình.
- Đặt ẩn phụ bằng một biến mới t.
Bước 2: Chuyển đổi phương trình:
- Thay thế biểu thức chứa ẩn phụ bằng biến t.
- Giải phương trình mới theo biến t.
Bước 3: Thay thế t và giải phương trình ban đầu:
- Thay giá trị tìm được của t vào ẩn phụ để tìm x.
- Giải phương trình tìm x.
Bài tập áp dụng
Giải phương trình: \(log_2 (x^2-2x+1) + \log_2 (x-1) = 1\)
Lời giải:
Đặt ẩn phụ: Đặt \( t= \log_2 (x-1)\)
Chuyển đổi phương trình:
\(t+\log_2 (x^2-2x+1)=1\) \(\log_2(x^2-2x+1) = 1-t\) \(x^2−2x+1=21−t\)Giải phương trình theo t:
\(x^2−2x+1−21−t=0\) \((x−1)^2−21−t=0\)Thay t và giải phương trình ban đầu:
\(\log_2 (x−1)^2−2^1- log_2 x-1=0\)Đặt \(u=\log_2 (x−1)\)
\(u^2 – 2^{1-u}= 0\)Giải phương trình này tìm u, sau đó thay \(u = \log_{2}(x-1)\) để tìm x.
Phương pháp mũ hóa
Phương pháp:
Bước 1: Viết lại phương trình logarit dưới dạng:
\(\log_a f(x) = g(x)\)Bước 2: Mũ hóa hai vế của phương trình:
\(f(x)=ag(x)\)Bước 3: Giải phương trình mũ để tìm x.
\(\log_{2} (x+1) =3\)Lời giải:
Bước 1: Viết lại phương trình:
\(\log_{2} (x+1) =3\)Bước 2: Mũ hóa hai vế:
\(x+1=2^3=8\)Bước 3: Giải phương trình:
\(x=7\)Bài tập áp dụng
Bài 1: Giải phương trình:
- \(\log_3 x+\log_4 2x=1\)
- \(\log_2 (x^2+2x)+log_2 (x+1)=2\)
- \(\log_x-12+\log_x+12=2\)
Bài 2: Giải phương trình logarit bằng phương pháp đồ thị:
Vẽ đồ thị của hai hàm số \(y=2x\) và \(y=3x\). Tìm nghiệm của phương trình 2x = 3x
Bài 3: Bài tập bất phương trình logarit:
Giải bất phương trình: \(\log_x+ 2^3 <2\).
Hiểu và nắm vững các công thức logarit là nền tảng quan trọng để học sinh giải quyết các bài toán logarit, đồng thời cũng là công cụ hữu ích để ứng dụng vào các lĩnh vực khác nhau như giải tích, thống kê, khoa học máy tính,…








