Trong toán học lớp 8, một trong những khái niệm cơ bản và quan trọng nhất là công thức tính diện tích tam giác. Đây là một khái niệm mà học sinh cần nắm vững để giải quyết các bài toán liên quan đến hình học. `Việc hiểu và áp dụng công thức này không chỉ giúp chúng ta hiểu rõ hơn về các đặc tính của tam giác mà còn là nền tảng cho việc học các khái niệm phức tạp hơn trong tương lai
Diện tích tam giác
Tam giác: là hình gồm ba cạnh và ba góc.
Diện tích tam giác: là phần diện tích được giới hạn bởi ba cạnh của tam giác.
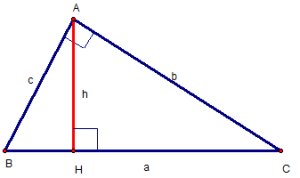
Tính chất
Diện tích tam giác bằng nửa tích của một cạnh với đường cao ứng với cạnh đó.
Diện tích hai tam giác có cùng chiều cao và chung cạnh đáy thì tỉ lệ với độ dài hai cạnh đáy.
Phân loại tam giác
Có một số cách phân loại tam giác dựa trên các tính chất khác nhau của nó:
Theo cạnh
- Tam giác đều: Có ba cạnh bằng nhau và ba góc bằng nhau (60 độ).
- Tam giác cân: Có ít nhất hai cạnh bằng nhau.
- Tam giác vuông: Có một góc vuông (90 độ).
Theo góc
- Tam giác nhọn: Có ba góc nhọn, tức là các góc đều nhỏ hơn 90 độ.
- Tam giác tù: Có một góc tù, tức là một góc lớn hơn 90 độ.
- Tam giác vuông: Đã đề cập ở trên, có một góc vuông.
Theo độ dài các cạnh
- Tam giác thường: Có ba cạnh và ba góc đều không bằng nhau.
- Tam giác đều, cân, vuông, tù…
Tổng hợp công thức tính diện tích tam giác
Diện tích tam giác
\(S = \frac{a * h}{2}\)
Trong đó:
S là diện tích tam giác.
a là độ dài một cạnh của tam giác.
h là độ dài đường cao ứng với cạnh a.
Diện tích tam giác vuông
\(S = \frac{a * b}{2}\)
Trong đó:
a và b là độ dài hai cạnh góc vuông của tam giác vuông.
Diện tích tam giác cân
\(S = \frac{a * h}{2}= \frac{b * h}{2}\)
Trong đó:
a và b là độ dài hai cạnh bên của tam giác cân.
h là độ dài đường cao ứng với cạnh đáy.
Diện tích tam giác đều
\(S = \frac{a² * \sqrt{3}}{4}\)
Trong đó:
a là độ dài cạnh của tam giác đều.
Ví dụ:
Cho tam giác ABC có cạnh đáy BC = 6 cm, đường cao AH = 5 cm. Tính diện tích tam giác ABC.
\(S = \frac{a * h}{2}=\frac{6 * 5}{2} = 15 cm²\)
Các dạng bài tập về diện tích hình tam giác
Dạng 1: Tính diện tích tam giác khi biết một cạnh và đường cao ứng với cạnh đó.
Ví dụ:
Cho tam giác ABC có cạnh đáy BC = 6 cm, đường cao AH = 5 cm. Tính diện tích tam giác ABC.
Giải:
Diện tích tam giác ABC là:
\(S = \frac{a * h}{2}=\frac{6 * 5}{2} = 15 cm²\)
Dạng 2: Tính diện tích tam giác vuông khi biết hai cạnh góc vuông.
Ví dụ:
Một tam giác vuông có hai cạnh góc vuông là 3 cm và 4 cm. Tính diện tích tam giác vuông.
Giải:
Diện tích tam giác vuông là:
\(S = \frac{a * h}{2}= \frac{3 *4}{2} = 6 cm²\)
Dạng 3: Tính diện tích tam giác cân khi biết cạnh đáy hoặc cạnh bên.
Ví dụ:
Một tam giác cân có cạnh đáy là 8 cm và cạnh bên là 10 cm. Tính diện tích tam giác cân.
Giải:
Cách 1:
Tính đường cao ứng với cạnh đáy:
\(h = \sqrt{a^2 – \left(\frac{b}{2}\right)^2} = \sqrt{10^2 – \left(\frac{8}{2}\right)^2} = \sqrt{84} = 2\sqrt{21}
cm\)
Diện tích tam giác cân là:
\(S = \frac{a \cdot h}{2} = \frac{8 \cdot 2\sqrt{21}}{2} = 8\sqrt{21} cm²\)
Cách 2:
Tính diện tích tam giác cân bằng cách chia thành hai tam giác vuông:
Diện tích tam giác cân là:
\(S = 2 \times \left(\frac{1}{2}\right) \times (b \cdot h) = 2 \times \left(\frac{1}{2}\right) \times (8 \cdot 2\sqrt{21}) = 8\sqrt{21} cm²\)
Dạng 4: Bài toán liên quan đến thực tế.
Ví dụ:
Một mảnh vườn hình tam giác có cạnh đáy là 10 m và chiều cao là 8 m. Người ta trồng rau trên mảnh vườn, cứ 1 m² thu hoạch được 2 kg rau. Hỏi trên mảnh vườn đó thu hoạch được bao nhiêu kg rau?
Giải:
Diện tích mảnh vườn là:
\(S = \frac{a * h}{2} = S = \frac{10 * 8}{2} = 40 m²\)
Số kg rau thu hoạch được trên mảnh vườn là:
40 * 2 = 80 kg
Bài tập về Diện tích hình tam giác lớp 8 (có lời giải chi tiết)
Bài 1:
Cho tam giác ABC có cạnh đáy BC = 6 cm, đường cao AH = 4 cm. Tính diện tích tam giác ABC.
Giải:
Diện tích tam giác ABC là:
\(S = \frac{a * h}{2} = S = \frac{6 *4}{2} = 12 cm²\)
Bài 2:
Cho tam giác ABC vuông tại A, biết AB = 3 cm và AC = 4 cm. Tính diện tích tam giác ABC.
Giải:
Diện tích tam giác ABC là:
\(S = \frac{a * h}{2} = S = \frac{3 *4}{2} = 6 cm²\)
Bài 3:
Cho tam giác ABC cân tại A, biết cạnh đáy BC = 8 cm và đường cao AH = 4 cm. Tính diện tích tam giác ABC.
Giải:
Diện tích tam giác ABC là:
\(S = \frac{a * h}{2} = S = \frac{8 *4}{2} = 16 cm²\)
Bài 4:
Một mảnh vườn hình tam giác có cạnh đáy là 12 m và chiều cao là 8 m. Người ta trồng rau trên mảnh vườn, cứ 1 m² thu hoạch được 3 kg rau. Hỏi trên mảnh vườn đó thu hoạch được bao nhiêu kg rau?
Giải:
Diện tích mảnh vườn là:
\(S = \frac{a * h}{2} = S = \frac{12* 8}{2} = 48 m²\)
Số kg rau thu hoạch được trên mảnh vườn là:
48 * 3 = 144 kg
Bài tập vận dụng
Bài 1:
Cho tam giác ABC có cạnh đáy BC = 7 cm và đường cao AH = 5 cm. Tính diện tích tam giác ABC.
Bài 2:
Cho tam giác ABC vuông tại A, biết AB = 4 cm và AC = 6 cm. Tính diện tích tam giác ABC.
Bài 3:
Cho tam giác ABC cân tại A, biết cạnh đáy BC = 10 cm và đường cao AH = 6 cm. Tính diện tích tam giác ABC.
Bài 4:
Một mảnh vườn hình tam giác có cạnh đáy là 15 m và chiều cao là 10 m. Người ta trồng rau trên mảnh vườn, cứ 1 m² thu hoạch được 2 kg rau. Hỏi trên mảnh vườn đó thu hoạch được bao nhiêu kg rau?
Bài 5:
Cho tam giác ABC có BC = 8 cm, đường cao AH = 5 cm và AD là đường phân giác (D thuộc BC). Biết BD = 3 cm. Tính diện tích tam giác ABD và diện tích tam giác ACD.
Bằng cách hiểu và áp dụng công thức này vào việc giải các bài tập, họ sẽ phát triển khả năng tư duy logic, kỹ năng tính toán, và sự tự tin trong học tập. Đồng thời, việc áp dụng công thức diện tích tam giác cũng giúp học sinh nhận biết và thấy được ứng dụng của toán học








