Chỉnh hợp là một chủ đề hay gây khó khăn cho học sinh lớp 11. Bài viết này ra đời nhằm mục đích giúp các bạn hiểu rõ hơn về chỉnh hợp, từ đó có thể giải quyết các bài tập một cách hiệu quả. Bài viết sẽ cung cấp cho các bạn kiến thức về các dạng bài tập thường gặp, phương pháp giải và các bí kíp để giải nhanh và chính xác.
Khái niệm chỉnh hợp
Chỉnh hợp chập k của n phần tử là cách sắp xếp k phần tử khác nhau lấy từ n phần tử cho trước theo một thứ tự nhất định.
Ví dụ:
Với tập hợp A = {1, 2, 3}, ta có các chỉnh hợp chập 2 của 3 phần tử:
- 12
- 13
- 21
- 23
- 31
- 32
Công thức tính chỉnh hợp
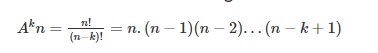
Số cách sắp xếp chỉnh hợp
Số cách sắp xếp k phần tử khác nhau lấy từ n phần tử cho trước là:
\(A_n^k = n! / (n – k)!\)
Ví dụ:
Với tập hợp A = {1, 2, 3}, số cách sắp xếp 2 phần tử từ 3 phần tử là:
\(A_3^2 = 3! / (3 – 2)! = 3! / 1! = 6\)
Tính chất của chỉnh hợp
Giao hoán:
Với hai chỉnh hợp bất kỳ P và Q, ta luôn có:
\(P ∩ Q = Ø\)
- Kết hợp:
Với ba chỉnh hợp bất kỳ P, Q và R, ta luôn có:
\((P ∩ Q) ∩ R = P ∩ (Q ∩ R)\)
Ứng dụng của chỉnh hợp
Chỉnh hợp được ứng dụng trong nhiều lĩnh vực như:
- Giải toán tổ hợp
- Giải mã
- Xác suất thống kê
- Tin học
Ví dụ:
1) Có 5 học sinh tham gia một cuộc thi. Hỏi có bao nhiêu cách chọn 3 học sinh để trao giải nhất, nhì, ba?
Lời giải:
Có 5 cách chọn học sinh cho vị trí thứ nhất, 4 cách chọn học sinh cho vị trí thứ hai và 3 cách chọn học sinh cho vị trí thứ ba.
Do đó, có 5 x 4 x 3 = 60 cách chọn 3 học sinh để trao giải nhất, nhì, ba.
2) Một công ty có 10 nhân viên. Hỏi có bao nhiêu cách chọn 3 nhân viên đi công tác?
Lời giải:
Có 10 cách chọn nhân viên thứ nhất, 9 cách chọn nhân viên thứ hai và 8 cách chọn nhân viên thứ ba.
Tuy nhiên, do thứ tự đi công tác không quan trọng, nên số cách chọn 3 nhân viên đi công tác là:
\(A_10^3 = 10! / (10 – 3)! = 10 x 9 x 8 = 720\)
Quy tắc đếm chỉnh hợp
Cho một tập hợp A bao gồm n phần tử; n≥1.
Một chỉnh hợp chập k các phần tử của tập hợp A là một cách sắp xếp k phần tử khác nhau của A trong đó 1<k<n và k N
Số chỉnh hợp được tính theo công thức: \(n!k!(n-k)!\)
Bài tập có lời giải chi tiết về chỉnh hợp
Bài tập 1:
Có 5 học sinh tham gia một cuộc thi. Hỏi có bao nhiêu cách chọn 3 học sinh để trao giải nhất, nhì, ba?
Lời giải:
Có 5 cách chọn học sinh cho vị trí thứ nhất, 4 cách chọn học sinh cho vị trí thứ hai và 3 cách chọn học sinh cho vị trí thứ ba.
Do đó, có 5 x 4 x 3 = 60 cách chọn 3 học sinh để trao giải nhất, nhì, ba.
Bài tập 2:
Một công ty có 10 nhân viên. Hỏi có bao nhiêu cách chọn 3 nhân viên đi công tác?
Lời giải:
Có 10 cách chọn nhân viên thứ nhất, 9 cách chọn nhân viên thứ hai và 8 cách chọn nhân viên thứ ba.
Tuy nhiên, do thứ tự đi công tác không quan trọng, nên số cách chọn 3 nhân viên đi công tác là:
\(A_10^3 = 10! / (10 – 3)! = 10 x 9 x 8 = 720\)Bài tập 3:
Có 10 lá cờ khác nhau được treo trên một hàng ngang. Hỏi có bao nhiêu cách xếp 5 lá cờ đầu tiên?
Lời giải:
Có 10 cách chọn lá cờ thứ nhất, 9 cách chọn lá cờ thứ hai, 8 cách chọn lá cờ thứ ba, 7 cách chọn lá cờ thứ tư và 6 cách chọn lá cờ thứ năm.
Do đó, có 10 x 9 x 8 x 7 x 6 = 15120 cách xếp 5 lá cờ đầu tiên.
Bài tập 4:
Từ tập hợp A = {1, 2, 3, 4, 5}, lập các số có 3 chữ số khác nhau. Hỏi có bao nhiêu số?
Lời giải:
Có 5 cách chọn chữ số thứ nhất, 4 cách chọn chữ số thứ hai và 3 cách chọn chữ số thứ ba.
Do đó, có 5 x 4 x 3 = 60 số có 3 chữ số khác nhau được lập từ tập hợp A.
Bài tập 5:
Có 6 học sinh nam và 4 học sinh nữ. Hỏi có bao nhiêu cách chọn 5 học sinh để tham gia một hoạt động, trong đó có ít nhất 2 học sinh nữ?
Lời giải:
Cách 1:
Có 2 trường hợp:
Trường hợp 1: Có 2 học sinh nữ và 3 học sinh nam.
Số cách chọn 2 học sinh nữ trong 4 học sinh nữ là:
\(C_4^2 = 4! / (2! * 2!) = 6\)
Số cách chọn 3 học sinh nam trong 6 học sinh nam là:
\(C_6^3 = 6! / (3! * 3!) = 20\)
Do đó, có 6 x 20 = 120 cách chọn 2 học sinh nữ và 3 học sinh nam.
Trường hợp 2: Có 3 học sinh nữ và 2 học sinh nam.
Số cách chọn 3 học sinh nữ trong 4 học sinh nữ là:
\(C_4^3 = 4! / (3! * 1!) = 4\)
Số cách chọn 2 học sinh nam trong 6 học sinh nam là:
\(C_6^2 = 6! / (2! * 4!) = 15\)
Do đó, có 4 x 15 = 60 cách chọn 3 học sinh nữ và 2 học sinh nam.
Tổng số cách chọn 5 học sinh để tham gia một hoạt động, trong đó có ít nhất 2 học sinh nữ là:
120 + 60 = 180
Cách 2:
Số cách chọn 5 học sinh bất kỳ trong 10 học sinh là:
\(C_{10}^5 = 10! / (5! * 5!) = 252\)
Số cách chọn 5 học sinh không có học sinh nữ là:
\(C_6^5 = 6! / (5! * 1!) = 6\)
Do đó, số cách chọn 5 học sinh để tham gia một hoạt động, trong đó có ít nhất 2 học sinh nữ là:
252 – 6 = 246
Chỉnh hợp là một chủ đề quan trọng, có nhiều ứng dụng thực tế. Hy vọng qua bài viết này, bạn đã có được những kiến thức nền tảng vững chắc để tiếp tục học tập và nghiên cứu các chủ đề toán học cao hơn.








