Bất đẳng thức Cosi (hay Cauchy) là một trong những bất đẳng thức quan trọng nhất trong chương trình Toán lớp 10. Bất đẳng thức này có nhiều ứng dụng trong việc giải toán, chứng minh các bất đẳng thức khác, và giải bài toán liên quan đến hình học.
Định nghĩa
Bất đẳng thức Cosi (Cauchy) cho hai số thực dương a và b:
\(√(ab) ≤ (a + b)/2\)
Dấu “=” xảy ra khi và chỉ khi a = b.
Hệ quả
Trung bình cộng – Trung bình nhân
\(√(ab) ≤ (a + b)/2\)
Tổng của một số dương với nghịch đảo của nó
\(a + 1/a ≥ 2\)
Bất đẳng thức AM-GM
Cho n số thực dương a1, a2, …, an, ta có:
\((a1 + a2 + … + an)/n ≥ √[n(a1a2…an)]\)
Chứng minh
Chứng minh bất đẳng thức Cosi
Cách 1: Sử dụng phương pháp biến đổi tương đương.
Cách 2: Sử dụng tính chất của vectơ.
Chứng minh hệ quả
Trung bình cộng – Trung bình nhân
- Ta có: \((a – b)^2 ≥ 0\)
- Khai triển, ta được: \(a^2 – 2ab + b^2 ≥ 0\)
- Chia hai vế cho 4, ta được: \((a + b)/2 – √(ab) ≥ 0\)
- Suy ra: \(√(ab) ≤ (a + b)/2\)
Tổng của một số dương với nghịch đảo của nó
Áp dụng bất đẳng thức Cosi cho a và 1/a, ta được:
\(√(a.1/a) ≤ (a + 1/a)/2\)
Suy ra: \(a + 1/a ≥ 2\)
Ví dụ
Ví dụ 1: Chứng minh rằng:
\(√(a^2 + b^2) ≥ √2ab\)
Lời giải:
- Áp dụng bất đẳng thức Cosi cho a và b, ta được:
\(√(ab) ≤ (a + b)/2\)
- Bình phương hai vế, ta được: \(ab ≤ (a^2 + 2ab + b^2)/4
- Suy ra: [latex]√(a^2 + b^2) ≥ √2ab\)
Ví dụ 2: Tìm giá trị nhỏ nhất của biểu thức:
\(P = x + y + 1/x + 1/y\)
Lời giải:
- Áp dụng bất đẳng thức Cosi cho x và 1/x, ta được:
\(x + 1/x ≥ 2\)
- Áp dụng bất đẳng thức Cosi cho y và 1/y, ta được:
\(y + 1/y ≥ 2\)
- Cộng hai bất đẳng thức trên, ta được:
\(P = x + y + 1/x + 1/y ≥ 4\)
- Dấu “=” xảy ra khi x = y = 1.
- Vậy giá trị nhỏ nhất của P là 4 khi x = y = 1.\
Dạng tổng quát của bất đẳng thức Cosi
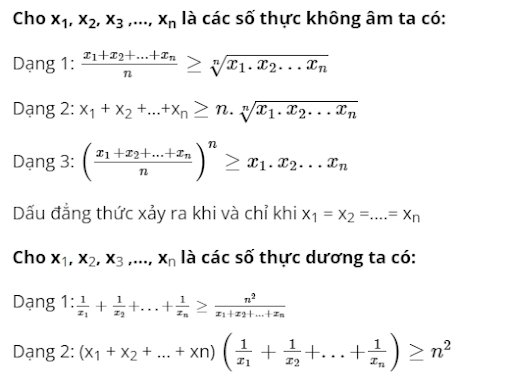
Các bất đẳng thức Cosi đặc biệt

Các dạng bài tập bất đẳng thức Cosi
Dạng 1: Chứng minh bất đẳng thức bằng cách áp dụng trực tiếp bất đẳng thức Cosi
Ví dụ: Chứng minh rằng:
\(√(a^2 + b^2) ≥ √2ab\)
Lời giải:
Áp dụng bất đẳng thức Cosi cho a và b, ta được:
\(√(ab) ≤ (a + b)/2\)
- Bình phương hai vế, ta được: \(ab ≤ (a^2 + 2ab + b^2)/4\)
- Suy ra: \(√(a^2 + b^2) ≥ √2ab\)
Dạng 2: Chứng minh bất đẳng thức bằng cách biến đổi tương đương
Ví dụ: Chứng minh rằng:
\(a + b + c ≥ √(ab + ac + bc)\)
Lời giải:
Biến đổi bất đẳng thức cần chứng minh:
\(a + b + c ≥ √(ab + ac + bc)\)
⇔ \((a + b + c)^2 ≥ ab + ac + bc\)
⇔ \(a^2 + b^2 + c^2 + 2ab + 2ac + 2bc ≥ ab + ac + bc\)
⇔ \(a^2 + b^2 + c^2 ≥ ab + ac + bc – 2ab – 2ac – 2bc\)
⇔ \(a^2 + b^2 + c^2 ≥ -ab – ac – bc\)
- Áp dụng bất đẳng thức Cosi cho a, b, c, ta được:
\(√(abc) ≤ (a + b + c)/3\)
- Bình phương hai vế, ta được: \(abc ≤ (a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)/9\)
- Suy ra: \(-ab – ac – bc ≤ -2√(abc) ≤ -2√[(a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)/9]\)
- Do đó, \(a^2 + b^2 + c^2 ≥ -ab – ac – bc\)
- Vậy \(a + b + c ≥ √(ab + ac + bc)\)
Dạng 3: Tìm giá trị nhỏ nhất hoặc lớn nhất của biểu thức bằng cách áp dụng bất đẳng thức Cosi.
Ví dụ: Tìm giá trị nhỏ nhất của biểu thức:
\(P = x + y + 1/x + 1/y\)
Lời giải:
Áp dụng bất đẳng thức Cosi cho x và 1/x, ta được:
x + 1/x ≥ 2
Áp dụng bất đẳng thức Cosi cho y và 1/y, ta được:
y + 1/y ≥ 2
Cộng hai bất đẳng thức trên, ta được:
P = x + y + 1/x + 1/y ≥ 4
- Dấu “=” xảy ra khi x = y = 1.
- Vậy giá trị nhỏ nhất của P là 4 khi x = y = 1.
Bài tập có lời giải về bất đẳng thức Cosi lớp 10
Bài 1: Chứng minh rằng:
\(√(a^2 + b^2) ≥ √2ab\)
Lời giải:
- Áp dụng bất đẳng thức Cosi cho a và b, ta được:
\(√(ab) ≤ (a + b)/2\)
- Bình phương hai vế, ta được: \(ab ≤ (a^2 + 2ab + b^2)/4
- Suy ra: [latex]√(a^2 + b^2) ≥ √2ab\)
Bài 2: Tìm giá trị nhỏ nhất của biểu thức:
P = x + y + 1/x + 1/y
Lời giải:
- Áp dụng bất đẳng thức Cosi cho x và 1/x, ta được:
x + 1/x ≥ 2
- Áp dụng bất đẳng thức Cosi cho y và 1/y, ta được:
y + 1/y ≥ 2
- Cộng hai bất đẳng thức trên, ta được:
P = x + y + 1/x + 1/y ≥ 4
- Dấu “=” xảy ra khi x = y = 1.
- Vậy giá trị nhỏ nhất của P là 4 khi x = y = 1.
Bài 3: Cho a, b, c là các số thực dương. Chứng minh rằng:
\(a + b + c ≥ √(ab + ac + bc)\)
Lời giải:
- Biến đổi bất đẳng thức cần chứng minh:
\(a + b + c ≥ √(ab + ac + bc)\)
⇔ \((a + b + c)^2 ≥ ab + ac + bc\)
⇔ \(a^2 + b^2 + c^2 + 2ab + 2ac + 2bc ≥ ab + ac + bc\)
⇔ \(a^2 + b^2 + c^2 ≥ ab + ac + bc – 2ab – 2ac – 2bc\)
⇔ \(a^2 + b^2 + c^2 ≥ -ab – ac – bc\)
- Áp dụng bất đẳng thức Cosi cho a, b, c, ta được:
\(√(abc) ≤ (a + b + c)/3\)
- Bình phương hai vế, ta được: \(abc ≤ (a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)/9\)
- Suy ra: \(-ab – ac – bc ≤ -2√(abc) ≤ -2√[(a^2 + b^2 + c^2 + 2ab + 2ac + 2bc)/9]\)
- Do đó, \(a^2 + b^2 + c^2 ≥ -ab – ac – bc\)
- Vậy \(a + b + c ≥ √(ab + ac + bc)\)
Bài viết đã trình bày một cách chi tiết về bất đẳng thức Cosi. Hy vọng những kiến thức và kỹ năng được cung cấp trong bài viết sẽ giúp học sinh giải quyết hiệu quả các bài toán liên quan đến dạng bất đẳng thức này.








