Tổ hợp lớp 11 là một cách chọn k phần tử bất kỳ từ n phần tử cho trước. Bài viết này sẽ giúp bạn hiểu rõ hơn về khái niệm tổ hợp, bao gồm các loại tổ hợp cơ bản, tính chất của chúng và cách biểu diễn tổ hợp.
Tổ hợp là gì?
Trong chương trình Toán học, tổ hợp là cách ta chọn những phần tử từ một nhóm lớn hơn mà không phân biệt thứ tự. Trong một vài trường hợp chúng ta còn có thể đếm được số tổ hợp.
Tổ hợp chập k của n phần tử được hiểu là số những nhóm gồm k phần tử được lấy ra từ n phần tử, mà giữa chúng chỉ khác nhau về thành phần cấu tạo chứ không quan trọng về thứ tự sắp xếp các phần tử.
Với mỗi một tập con gồm k phần tử của tập hợp gồm n phần tử (n > 0) được gọi là một tổ hợp chập k của n.
Công thức tổ hợp
Ta có tổ hợp chập k của n phần tử (1 ≤ k ≤ n )
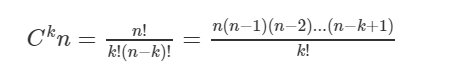
Số cách chọn tổ hợp
Số cách chọn k phần tử bất kỳ từ n phần tử là:
\(C_n^k = n! / (k!(n – k)!)\)

Tính chất tổ hợp
- Giao hoán:
Với hai tổ hợp bất kỳ P và Q, ta luôn có:
P ∩ Q = Ø
- Kết hợp:
Với ba tổ hợp bất kỳ P, Q và R, ta luôn có:
(P ∩ Q) ∩ R = P ∩ (Q ∩ R)
Mối quan hệ giữa tổ hợp, chỉnh hợp và hoán vị
Thông qua định nghĩa, chúng ta có thể thấy tổ hợp, chỉnh hợp và hoán vị có một mối liên hệ với nhau.
Cụ thể một chỉnh hợp chập k của n được tạo thành bằng cách thực hiện 2 bước như sau:
- Bước 1: Lấy 1 tổ hợp chập k của n phần tử.
Bước 2: Hoán vị k phần tử.
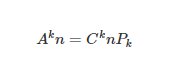
Do đó chúng ta có công thức liên hệ giữa chỉnh hợp, tổ hợp, hoán vị như sau:
Quy tắc đếm tổ hợp
Cho một tập hợp A bao gồm có n phần tử với n > 0 Một tổ hợp chập k bất kì của các phần tử thuộc tập hợp A là một tập hợp con có k phần tử của A / 0 k n ; k N.
Số tổ hợp được tính theo công thức sau: n!(n-k)!
Bài tập tổ hợp có lời giải chi tiết
Bài 1:

Bài 2:

Bài 3:

Bài tập 4:
Từ tập hợp A = {1, 2, 3, 4, 5}, lập các số có 3 chữ số khác nhau. Hỏi có bao nhiêu số?
Lời giải:
Có 5 cách chọn chữ số thứ nhất, 4 cách chọn chữ số thứ hai và 3 cách chọn chữ số thứ ba.
Do đó, có 5 x 4 x 3 = 60 số có 3 chữ số khác nhau được lập từ tập hợp A.
Bài tập 5:
Có 6 học sinh nam và 4 học sinh nữ. Hỏi có bao nhiêu cách chọn 5 học sinh để tham gia một hoạt động, trong đó có ít nhất 2 học sinh nữ?
Cách 1:
Có 2 trường hợp:
- Trường hợp 1: Có 2 học sinh nữ và 3 học sinh nam.
Số cách chọn 2 học sinh nữ trong 4 học sinh nữ là:
\(C_4^2 = 4! / (2! * 2!) = 6\)
Số cách chọn 3 học sinh nam trong 6 học sinh nam là:
\(C_6^3 = 6! / (3! * 3!) = 20\)
Do đó, có 6 x 20 = 120 cách chọn 2 học sinh nữ và 3 học sinh nam.
- Trường hợp 2: Có 3 học sinh nữ và 2 học sinh nam.
Số cách chọn 3 học sinh nữ trong 4 học sinh nữ là:
\(C_4^3 = 4! / (3! * 1!) = 4\)
Số cách chọn 2 học sinh nam trong 6 học sinh nam là:
\(C_6^2 = 6! / (2! * 4!) = 15\)
Do đó, có 4 x 15 = 60 cách chọn 3 học sinh nữ và 2 học sinh nam.
Tổng số cách chọn 5 học sinh để tham gia một hoạt động, trong đó có ít nhất 2 học sinh nữ là:
120 + 60 = 180
Cách 2:
Số cách chọn 5 học sinh bất kỳ trong 10 học sinh là:
\(C_{10}^5 = 10! / (5! * 5!) = 252\)
Số cách chọn 5 học sinh không có học sinh nữ là:
\(C_6^5 = 6! / (5! * 1!) = 6\)
Do đó, số cách chọn 5 học sinh để tham gia một hoạt động, trong đó có ít nhất 2 học sinh nữ là:
252 – 6 = 246
Bài tập tổ hợp tự luyện
Bài 1: Có 25 học sinh tham gia một cuộc thi. Hỏi có bao nhiêu cách chọn 6 học sinh để trao giải nhất, nhì, ba, tư, năm, sáu?
Bài 2: Một công ty có 21 nhân viên. Hỏi có bao nhiêu cách chọn 7 nhân viên đi công tác?
Bài 3: Có 18 lá cờ khác nhau được treo trên một hàng ngang. Hỏi có bao nhiêu cách xếp 7 lá cờ đầu tiên?
Bài 4: Từ tập hợp A = {1, 2, 3, 4, 5, 6, 7, 8, 9}, lập các số có 7 chữ số khác nhau. Hỏi có bao nhiêu số?
Bài 5: Có 10 học sinh nam và 6 học sinh nữ. Hỏi có bao nhiêu cách chọn 9 học sinh để tham gia một hoạt động, trong đó có ít nhất 5 học sinh nữ?
Hàm số lượng giác là một chủ đề quan trọng, có nhiều ứng dụng thực tế. Hy vọng qua bài viết này, bạn đã có được những kiến thức nền tảng vững chắc để tiếp tục học tập và nghiên cứu các chủ đề toán học cao hơn.








