Tính diện tích hình thang là một trong những kiến thức cơ bản của môn Toán lớp 8. Việc nắm vững cách tính diện tích hình thang giúp học sinh giải quyết được nhiều dạng bài tập khác nhau. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về công thức tính diện tích hình thang cũng như các dạng bài tập thường gặp liên quan đến diện tích hình thang.
Định nghĩa hình thang
Hình thang: là tứ giác có hai cạnh đối diện song song.
Chiều cao: là đoạn thẳng vuông góc với hai cạnh đáy, nối hai điểm trên hai cạnh đáy.
Diện tích hình thang: là phần diện tích được giới hạn bởi hình thang.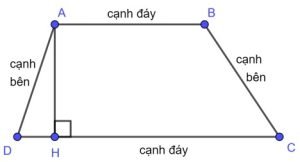
Tính chất của diện tích hình thang
Diện tích hình thang bằng trung bình cộng của hai đáy nhân với chiều cao.
Diện tích hai hình thang có cùng chiều cao và chung cạnh đáy thì tỉ lệ với độ dài hai cạnh đáy.
Công thức tính diện tích hình thang
Công thức diện tích hình thang
\(S = \frac{(a + b) * h}{2}\)Trong đó:
S là diện tích hình thang.
a và b là độ dài hai cạnh đáy của hình thang.
h là độ dài đường cao của hình thang.
Công thức diện tích hình thang vuông
Hình thang vuông: là hình thang có một góc vuông.
Công thức diện tích hình thang vuông:
\(S = \frac{(a + b) * h}{2} =\frac{ab}{2}\)Trong đó:
a và b là độ dài hai cạnh góc vuông của hình thang vuông.
Hình thang cân: là hình thang có hai cạnh bên bằng nhau.
Công thức diện tích hình thang cân
\(S = \frac{(a + b) * h}{2}\)Trong đó:
a và b là độ dài hai cạnh đáy của hình thang cân.
h là độ dài đường cao của hình thang cân.
Ví dụ
Cho hình thang ABCD có cạnh đáy AB = 8 cm, cạnh đáy CD = 10 cm, đường cao AH = 5 cm. Tính diện tích hình thang ABCD.
\(S = \frac{(a + b) * h}{2} = \frac{(8 + 10) * 5}{2}= 90 cm²\)Dạng 1: Tính diện tích hình thang khi biết hai cạnh đáy và đường cao.
Ví dụ:
Cho hình thang ABCD có cạnh đáy AB = 6 cm, cạnh đáy CD = 8 cm, đường cao AH = 4 cm. Tính diện tích hình thang ABCD.
Giải:
Diện tích hình thang ABCD là:
\(S = \frac{(a + b) * h}{2} = \frac{(6 + 8) * 4}{2} = 56 cm²\)Dạng 2: Tính diện tích hình thang khi biết hai cạnh góc vuông (hình thang vuông).
Ví dụ:
Một hình thang vuông có hai cạnh góc vuông là 3 cm và 4 cm. Tính diện tích hình thang vuông.
Giải:
Diện tích hình thang vuông là:
\(S = \frac{ab}{2} =\frac{3.4}{2} = 6 cm²\)Dạng 3: Tính diện tích hình thang khi biết cạnh đáy và cạnh bên (hình thang cân).
Ví dụ:
Một hình thang cân có cạnh đáy là 8 cm và cạnh bên là 10 cm. Tính diện tích hình thang cân.
Giải:
Cách 1:
Tính đường cao ứng với cạnh đáy:
\(h = \sqrt{a^2 – \left(\frac{b}{2}\right)^2} = \sqrt{10^2 – \left(\frac{8}{2}\right)^2} = \sqrt{84} = 2\sqrt{21}\) (cm)
Diện tích hình thang cân là:
\(h = \sqrt{a^2 – \left(\frac{b}{2}\right)^2} = \sqrt{10^2 – \left(\frac{8}{2}\right)^2} = \sqrt{84} = 2\sqrt{21}\) (cm)
Cách 2:
Tính diện tích hình thang cân bằng cách chia thành hai tam giác vuông:
Diện tích tam giác vuông là:
\(S = \frac{1}{2} \times (b \cdot h) = \frac{1}{2} \times (8 \cdot 2\sqrt{21}) = 8\sqrt{21} (cm^2)\)Diện tích hình thang cân là:
\(S = 2 \times S = 2 \times 8\sqrt{21} = 16\sqrt{21}cm²\)Dạng 4: Bài toán liên quan đến thực tế.
Ví dụ:
Một mảnh vườn hình thang có cạnh đáy lớn là 10 m, cạnh đáy bé là 8 m và chiều cao là 5 m. Người ta trồng rau trên mảnh vườn, cứ 1 m² thu hoạch được 2 kg rau. Hỏi trên mảnh vườn đó thu hoạch được bao nhiêu kg rau?
Giải:
Diện tích mảnh vườn là:
\(S = \frac{(a + b) \times h}{2} = \frac{(10 + 8) \times 5}{2} = 90 m²\)Số kg rau thu hoạch được trên mảnh vườn là:
90 * 2 = 180 kg
Bài tập về diện tích hình thang có lời giải
Bài 1: Cho hình thang ABCD có AB // CD, AB = 10 cm, CD = 14 cm, AH = 8 cm (h.141). Tính diện tích hình thang ABCD.
Giải:
Diện tích hình thang ABCD là:
\(S = \frac{(a + b) \times h}{2} = \frac{(10 + 14) \times 8}{2} = 96 (cm²)\)Bài 2: Tính diện tích hình thang ABCD, biết AB = 6 cm, CD = 10 cm, AD = 5 cm, AC = 7 cm (h.142).
Giải:
Cách 1:
Nối BD.
Diện tích tam giác ABD là:
S = (1/2) * (AB * AD) = (1/2) * (6 * 5) = 15 (cm²)
Diện tích tam giác BDC là:
S = (1/2) * (BC * CD) = (1/2) * (10 * 7) = 35 (cm²)
Diện tích hình thang ABCD là:
S = S + S = 15 + 35 = 50 (cm²)
Cách 2:
Kẻ đường cao AH của hình thang ABCD.
Diện tích tam giác AHD là:
S = (1/2) * (AH * AD) = (1/2) * (h * 5) = (5 * h)/2
Diện tích tam giác BHC là:
S = (1/2) * (BH * BC) = (1/2) * (h * 10) = (10 * h)/2
Diện tích hình thang ABCD là:
S = S + S = (5 * h)/2 + (10 * h)/2 = (15 * h)/2
Ta có: S = 50 cm² và AB = 6 cm, CD = 10 cm
Diện tích hình thang ABCD là:
S = (15 * h)/2 = 50 => h = (50 * 2)/15 = 6,67 (cm)
Vậy diện tích hình thang ABCD là 50 cm².
Bài 3: Một mảnh vườn hình thang có đáy lớn 30 m, đáy bé 20 m và chiều cao 15 m. Người ta trồng rau trên mảnh vườn, cứ 1 m² thu hoạch được 10 kg rau. Hỏi trên mảnh vườn đó thu hoạch được bao nhiêu ki-lô-gam rau?
Giải:
Diện tích mảnh vườn là:
S = [(a + b) * h]/2 = [(30 + 20) * 15]/2 = 750 (m²)
Số ki-lô-gam rau thu hoạch được trên mảnh vườn là:
750 * 10 = 7500 (kg)
Vậy trên mảnh vườn đó thu hoạch được 7500 kg rau.
Việc nắm vững các công thức tính diện tích hình thang là rất quan trọng để giải các bài toán liên quan đến hình thang. Bài viết này hy vọng đã cung cấp cho bạn những thông tin hữu ích về diện tích hình thang.








