Hai tam giác đồng dạng là hai tam giác có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ với nhau. Khái niệm này đóng vai trò quan trọng trong chương trình Toán học lớp 8 và có nhiều ứng dụng thực tế trong các lĩnh vực như đo lường, bản đồ, kiến trúc, v.v.Bài viết này sẽ trình bày kiến thức về hai tam giác đồng dạng, bao gồm định nghĩa, các trường hợp đồng dạng, tính chất, hệ quả và ứng dụng thực tế.
Định nghĩa hai tam giác đồng dạng
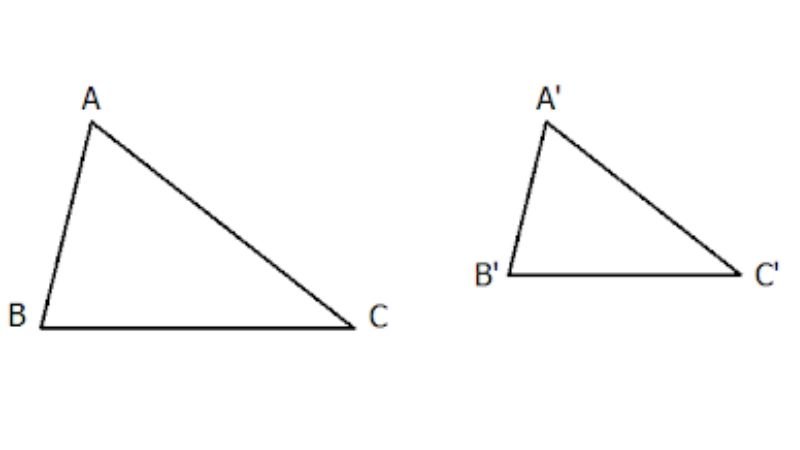
Hai tam giác được gọi là đồng dạng nếu chúng có các góc tương đương nhau và các tỉ lệ giữa độ dài các cạnh tương ứng là như nhau.
Cụ thể, hai tam giác ABC và DEF được coi là đồng dạng nếu:
- Góc A tương đương với góc D.
- Góc B tương đương với góc E.
- Góc C tương đương với góc F.
Tỉ lệ giữa độ dài các cạnh tương ứng là như nhau, tức là:
\(\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}\)Khi hai tam giác đồng dạng, chúng có hình dạng giống nhau, chỉ khác về kích thước. Điều này có nghĩa là một tam giác có thể được thu nhỏ hoặc phóng to mà không làm thay đổi hình dạng của nó.
Việc hiểu và sử dụng các thuộc tính của tam giác đồng dạng là quan trọng trong nhiều lĩnh vực của toán học và các ứng dụng thực tế như trong hình học, vật lý, và kỹ thuật.
Trường hợp đồng dạng
Trường hợp cạnh – cạnh (C-C):
Hai tam giác có ba cặp cạnh tương ứng tỉ lệ thì hai tam giác đó đồng dạng.
Ký hiệu: ΔABC∽ΔDEF
Điều kiện:
\(\frac{AB}{DE} = \frac{AC}{DF} = \frac{BC}{EF}\)Ví dụ:
Cho hai tam giác ABC và DEF có:
Ví dụ:
Cho hai tam giác ABC và DEF có:
\(\frac{AB}{AD} = \frac{AC}{DF} = \frac{BC}{EF} = k\)Khi đó, hai tam giác ABC và DEF đồng dạng theo trường hợp cạnh – cạnh
Trường hợp cạnh – góc – cạnh (C-G-):
Hai tam giác có hai cặp cạnh tương ứng tỉ lệ và hai góc tương ứng bằng nhau thì hai tam giác đó đồng dạng.
Ký hiệu:
ΔABC∽ΔDEF
Điều kiện:
\(\frac{AB}{DE} = \frac{AC}{DF}\)Góc A = góc D
Khi đó, hai tam giác ABC và DEF đồng dạng theo trường hợp cạnh – góc.
Trường hợp góc – góc (G-G):
Hai tam giác có hai góc tương ứng bằng nhau thì hai tam giác đó đồng dạng.
Ký hiệu:
ΔABC∽ΔDEF
góc A = góc D
góc B = góc E
Khi đó, hai tam giác ABC và DEF đồng dạng theo trường hợp góc – góc.
Lưu ý:
Ba trường hợp đồng dạng là những định lý quan trọng trong chương trình Toán học lớp 8.
Việc nắm vững kiến thức về ba trường hợp đồng dạng sẽ giúp bạn giải quyết các bài toán liên quan đến hình tam giác một cách hiệu quả và chính xác.
Tính chất tam giác đồng dạng
Tỉ số các cạnh tương ứng bằng nhau:
Cho hai tam giác ABC và DEF đồng dạng, ta có:
\(\frac{AB}{DE} = \frac{AC}{DF} = \frac{BC}{EF} = k\)Với k là hằng số.
Tỉ số các đường phân giác tương ứng bằng nhau:
Cho hai tam giác ABC và DEF đồng dạng, ta có:
\(\frac{AD}{DE} = \frac{AB}{DE} = K\).
\(\frac{AE}{DF} = \frac{AC}{DF} = K\).
\(\frac{AF}{EF} = \frac{BC}{EF} = K\)Tỉ số các đường cao tương ứng bằng nhau:
Cho hai tam giác ABC và DEF đồng dạng, ta có:
\(\frac{AH}{DH} = \frac{AB}{DE} = K\).
\(\frac{AK}{EK} = \frac{AC}{DF} = K\).
\(\frac{AL}{EL} = \frac{BC}{EF} = K\)Tỉ số diện tích tương ứng bằng bình phương tỉ số đồng dạng:
Cho hai tam giác ABC và DEF đồng dạng, ta có:
\(\frac{S_{ABC}}{S_{DEF}} = \left(\frac{AB}{DE}\right)^2 = K^2\)Lưu ý: Các tính chất của hai tam giác đồng dạng giúp ta giải quyết các bài toán liên quan đến hình tam giác một cách hiệu quả và chính xác.
Ngoài ra, bạn có thể tham khảo thêm các tài liệu khác để nâng cao kiến thức và kỹ năng giải bài tập về hai tam giác đồng dạng.
Hệ quả
Hệ quả của tam giác đồng dạng là những tính chất được suy ra từ định nghĩa của tam giác đồng dạng.
Dưới đây là một số hệ quả quan trọng của tam giác đồng dạng:
Hệ quả về đường phân giác:
Đường phân giác trong của một tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề.
Hệ quả về đường trung tuyến:
Đường trung tuyến của một tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề.
Hệ quả về đường cao:
Đường cao của một tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề.
Hệ quả về diện tích:
Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.
Hệ quả về các đường đặc biệt khác:
Ngoài ra, còn có một số hệ quả khác của tam giác đồng dạng liên quan đến các đường đặc biệt khác như đường phân giác ngoài, đường trung trực, đường tròn nội tiếp, đường tròn ngoại tiếp, v.v.
Lưu ý: Các hệ quả của tam giác đồng dạng giúp ta giải quyết các bài toán liên quan đến hình tam giác một cách hiệu quả và chính xác.
Tóm lại, hai tam giác đồng dạng là một chủ đề quan trọng trong chương trình Toán học lớp 8. Việc nắm vững kiến thức về chủ đề này sẽ giúp bạn giải quyết các bài toán liên quan đến hình tam giác một cách hiệu quả và chính xác. Ngoài ra, bạn có thể tham khảo thêm các tài liệu khác để nâng cao kiến thức và kỹ năng giải bài tập về hai tam giác đồng dạng. Hy vọng bài viết này hữu ích với bạn!