Tiên đề Ơ-clit về đường thẳng song song là một trong những khái niệm cơ bản và quan trọng trong môn Toán học lớp 7. Nó đóng vai trò nền tảng cho nhiều định lý, tính chất và bài toán liên quan đến đường thẳng và góc.
Tiên đề Ơ-clit về đường thẳng song song
Qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Cách diễn đạt khác:
Cho điểm A nằm ngoài đường thẳng a. Chỉ có một đường thẳng b đi qua A và song song với a.
Không có hai đường thẳng nào cùng song song với một đường thẳng thứ ba.
Dấu hiệu nhận biết hai đường thẳng song song
Dấu hiệu dựa vào một đường thẳng cắt hai đường thẳng: Nếu một đường thẳng cắt hai đường thẳng khác và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì hai đường thẳng đó song song với nhau.
Dấu hiệu dựa vào tính chất của hai đường thẳng song song: Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
Dấu hiệu dựa vào góc kề bù: Nếu hai đường thẳng cắt nhau tạo thành hai góc kề bù mà một trong hai góc đó bằng 90° thì hai đường thẳng đó song song với nhau.
Dấu hiệu dựa vào góc trong cùng phía: Nếu hai đường thẳng cắt nhau tạo thành hai góc trong cùng phía mà hai góc đó bù nhau thì hai đường thẳng đó song song với nhau.
Tính chất của hai đường thẳng song song
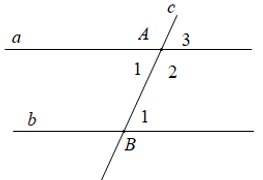
Hai góc so le trong:
Là hai góc nằm ở hai phía của đường thẳng thứ ba, so le với nhau.
Ví dụ: ∠A và ∠B’ trong hình vẽ.
Hai góc đồng vị:
Là hai góc nằm ở hai phía của đường thẳng thứ ba, cùng vị trí với nhau (cùng nằm ở vị trí trên hoặc dưới đường thẳng thứ ba).
Ví dụ: ∠A và ∠C’ trong hình vẽ.
Hai góc trong cùng phía:
Là hai góc nằm ở cùng một phía của đường thẳng thứ ba, trong cùng một góc bẹt.
Ví dụ: ∠B và ∠C’ trong hình vẽ.
Chứng minh
Chứng minh hai góc so le trong bằng nhau
Giả sử a // b.
Ta có: ∠AOC + ∠BOC = 180° (hai góc kề bù)
Suy ra: ∠BOC = 180° – ∠AOC (1)
Lại có: ∠A’OB + ∠B’OC = 180° (hai góc kề bù)
Suy ra: ∠B’OC = 180° – ∠A’OB (2)
Từ (1) và (2), suy ra: ∠BOC = ∠B’OC
Mà ∠BOC và ∠B’OC là hai góc so le trong
Vậy ∠A = ∠B’ (đpcm)
Chứng minh hai góc đồng vị bằng nhau
Giả sử a // b.
Ta có: ∠AOC + ∠A’OB = 180° (hai góc trong cùng phía)
Suy ra: ∠A’OB = 180° – ∠AOC (1)
Lại có: ∠C’OD + ∠B’OC = 180° (hai góc trong cùng phía)
Suy ra: ∠B’OC = 180° – ∠C’OD (2)
Từ (1) và (2), suy ra: ∠A’OB = ∠B’OC
Mà ∠A’OB và ∠B’OC là hai góc đồng vị
Vậy ∠A = ∠C’ (đpcm)
Chứng minh hai góc trong cùng phía bù nhau
Giả sử a // b.
Ta có: ∠AOC + ∠BOC = 180° (hai góc kề bù)
Vậy ∠BOC = 180° – ∠AOC (đpcm)
Bài tập trắc nghiệm có lời giải
Bài 1: Cho hình vẽ dưới đây, biết c. Tính x, y
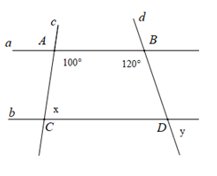
- x = 80° ; y = 80°
- x = 60° ; y = 80°
- x = 80° ; y = 60°
- x = 60° ; y = 60°
Giải
Vì a//bnên ∠BAC + ∠ACD=180° (hai góc trong cùng phía bù nhau)
Suy ra 100° + x = 180° ⇒ x = 80°
Tương tự ta có: ∠ABD+ ∠CDB=180° ⇒ ∠CDB = 60°
Suy ra y = ∠CDB = 60° (hai góc đối đỉnh)
Vậy x = 80°; y = 60°.
Bài 2: Cho hình vẽ sau, biết x // y và ∠M1 = 55°. Tính ∠N1
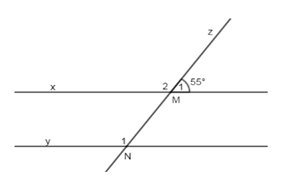
- 55°
- 35°
- 60°
- 125°
Giải
Ta có: ∠M₁+ ∠M₂ = 180° => ∠M₂ =180°- 55° = 125° (kề bù)
Vì x//y(gt) => ∠M₂ = ∠N₁ = 125° (hai góc đồng vị)
Chọn đáp án D
Bài tập tự luận có lời giải
Bài 1: Hai đường thẳng xx’ và yy’ song song với nhau bị cắt bở một cát tuyến tại 2 điểm A và B. Gọi At là tia phân giác của ∠xAB
- a) Tia At có cắt đường thẳng yy’ hay không? Vì sao?
- b) Cho ∠xAB = 80°. Tính ∠ACB = ?
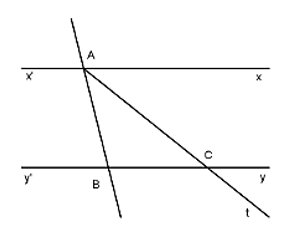
Đáp án
- a) Giả sử At không cắt yy’
Suy ra AC // yy’ .
Theo tiên đề Ơclit thì AC trùng với xx’
Điều này là vô nghĩa nên At phải cắt yy’ tại C.
- b) Ta có:
∠XAt=\(\frac{1}{2} ∠XAB= \frac{1}{2}80°= 40°\) (At là tia phân giác ∠xAB)
Mà ∠xAt = ∠ACB (so le trong)
Vậy ∠ACB = 40°
Bài 2: Cho hình bên, biết ∠A = 50° và ∠B = 140°, Ax // By’. Chứng minh ∠AOB = 90°
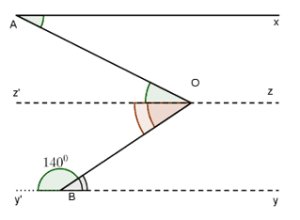
Giải
Kẻ qua O đường thẳng Oz // Ax
ta có: ∠AOz: =∠XAO = 50° (so le trong)
Lại có: ∠OBy = 140°
∠OBy = 180°-140° 40° = 40
Mặt khác ta lại có: Oz // Ax⇒ Oz // By
∠BOz’ = ∠OBy = 40° (góc so le trong)
Do đó:∠AOz = ∠z’OB = 50° +40° = 90° hay ∠AOB = 90° .
Vậy ∠AOB = 90° (đpcm)
Qua bài học này, chúng ta đã tìm hiểu về Tiên đề Ơ-clit về đường thẳng song song, cũng như các tính chất của hai đường thẳng song song. Nắm vững kiến thức này sẽ giúp các bạn giải quyết nhiều bài toán hình học một cách dễ dàng.








