Đồ thị hàm số y = ax (a ≠ 0) là một công cụ hữu ích giúp chúng ta biểu diễn trực quan mối quan hệ giữa hai đại lượng x và y. Bài học này sẽ giới thiệu cho các bạn cách vẽ đồ thị hàm số y = ax, từ đó giúp các bạn hiểu rõ hơn về mối quan hệ giữa hai đại lượng và giải các bài toán liên quan.
Đồ thị hàm số \(y = ax(a ≠ 0)\)
Đồ thị hàm số \(y = a(x)\) là tập hợp tất cả các điểm M(x; y) trên mặt phẳng tọa độ sao cho y = a(x).
Cách vẽ đồ thị hàm số
- Lập bảng giá trị
- Xác định các điểm đặc biệt (giao điểm với trục Ox, Oy)
- Vẽ đường cong đi qua các điểm đã xác định
Một số dạng đồ thị hàm số thường gặp
Đường thẳng: \(y = ax + b (a ≠ 0)\)
Parabol: \(y = ax^2 + bx + c (a ≠ 0)\)
Đường hyperbol: \(y = \frac{a}{x}\) (a ≠ 0)[/latex]
Tính chất của đồ thị hàm số y = ax
Đồ thị của hàm số \(y = ax (a ≠ 0)\) là đường thẳng đi qua gốc tọa độ.
Đồ thị của hàm số \(vy = x^2\) là parabol.
Đồ thị của hàm số \(y = \frac{1}{x}\) là đường hyperbol.
Cách vẽ đồ thị hàm số y = ax
Bước 1: Lập bảng giá trị
Chọn một số giá trị x bất kỳ (thường là -2, -1, 0, 1, 2).
Thay giá trị x vào hàm số y = ax để tính giá trị y tương ứng.
Ghi kết quả vào bảng giá trị.
Bước 2: Xác định các điểm đặc biệt
Điểm A(0; 0) là điểm mà đồ thị đi qua gốc tọa độ.
Điểm B(1; a) là điểm mà đồ thị đi qua giao điểm của trục Ox và đường thẳng y = a.
Bước 3: Vẽ đường biểu diễn
Nối các điểm A và B bằng một đường thẳng.
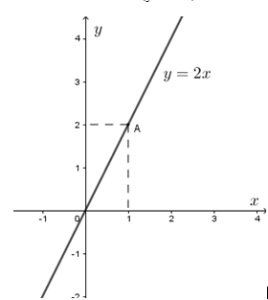
Ví dụ: Vẽ đồ thị hàm số \(y = 2x\)
Bước 1: Lập bảng giá trị
| x | y = 2x |
| -2 | -4 |
| -1 | -2 |
| 0 | 0 |
| 1 | 2 |
| 2 | 4 |
Bước 2: Xác định các điểm đặc biệt
A(0; 0)
B(1; 2)
Bước 3: Vẽ đường biểu diễn
Nối các điểm A và B bằng một đường thẳng.
Đường biểu diễn:
Các dạng toán thường gặp bài đồ thị hàm số \(y = ax\)
Dạng 1: Vẽ đồ thị hàm số \(y = ax (a ≠ 0)\)
Phương pháp giải:
Bước 1: Lập bảng giá trị.
Bước 2: Xác định các điểm đặc biệt.
Bước 3: Vẽ đường biểu diễn.
Ví dụ: Vẽ đồ thị hàm số \(y = 2x\).
Dạng 2: Xác định hàm số y = ax biết đồ thị của nó đi qua một điểm M(x₀; y₀) cho trước.
Phương pháp giải:
Thay tọa độ điểm M vào phương trình \(y = ax\).
Giải phương trình để tìm a.
Vẽ đồ thị hàm số \(y = ax\).
Ví dụ: Xác định hàm số \(y = ax\) biết đồ thị của nó đi qua điểm M(2; 4).
Dạng 3: Tìm giá trị của hàm số y = ax tại một giá trị cho trước của biến x.
Phương pháp giải:
Thay giá trị x vào hàm số \(y = ax\).
Tính giá trị y.
Ví dụ: Tìm giá trị của hàm số y = 3x tại x = 2.
Dạng 4: Giải bài toán liên quan đến đồ thị hàm số y = ax.
Phương pháp giải:
Phân tích đề bài: Xác định các đại lượng, mối quan hệ giữa các đại lượng, yêu cầu của bài toán.
Biểu diễn các đại lượng bằng đồ thị hàm số.
Giải bài toán bằng các kiến thức về đồ thị hàm số.
Kiểm tra kết quả: Kiểm tra xem kết quả có hợp lý hay không.
Dạng 5: Cho biết giá trị của hàm số. Yêu cầu tính giá trị của biến số
Phương pháp giải: Thay giá trị của hàm số vào đồ thị hàm số y=ax, từ đó tìm ra giá trị của biến số
Ví dụ: Cho hàm số y = 39x. Hãy tìm giá trị của biến số x biết giá trị của hàm số là y = 78
Giải:
Ta có: y = 39x = 78 ⇒ x = 2
Vậy giá trị của biến số x là: x = 2
Dạng 6: Cho giá trị của biến số, tìm giá trị của hàm số
Phương pháp giải: Thay giá trị của biến số vào hàm số y=ax để tìm ra giá trị của hàm số đó.
Ví dụ: Cho hàm số y = 5x. Hãy tính y(2); y(-9)
Giải:
Ta có: y(2) = 5.2 = 10
y(-9) = 5.(-9) = -45
Dạng 7: Bài toán về xét sự đồng biến hay nghịch biến của hàm số y=ax
Phương pháp giải: Hàm số y=ax là hàm số đồng biến khi a > 0 và là hàm số nghịch biến khi a < 0
Ví dụ: Hãy xét tính đồng biến, nghịch biến của các hàm số sau:
- y = 2022x
- y = -10x
Giải:
- Ta có: a = 2022 > 0 nên hàm số y = 2022x là hàm số đồng biến
- Ta có: a = -10 < 0 nên hàm số y = -10x là hàm số nghịch biế
Hy vọng các bạn đã nắm vững cách vẽ đồ thị hàm số y = ax và ứng dụng kiến thức vào giải các bài toán liên quan.








