Hình nón cụt là một phần của hình nón được tạo thành bởi mặt cắt song song với mặt đáy. Tính toán thể tích hình nón cụt là một kỹ năng quan trọng trong toán học và có nhiều ứng dụng thực tế.
Hình nón cụt là gì?
Hình nón cụt là phần hình nón còn lại sau khi cắt nón bởi một mặt phẳng song song với mặt đáy.
Hình nón cụt được tạo thành bởi hai phần:
Phần đáy nhỏ: là hình tròn với bán kính r.
Phần thân: là một hình nón cụt có đường cao h và bán kính đáy lớn R.
Công thức tính thể tích hình nón cụt
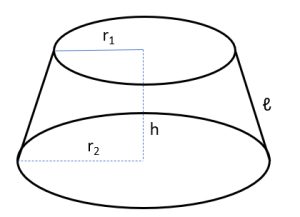
\(V = \frac{1}{3}π.h(R² + Rr + r²)\)
trong đó:
V là thể tích của hình nón cụt.
h là chiều cao của hình nón cụt.
R là bán kính đáy lớn của hình nón cụt.
r là bán kính đáy nhỏ của hình nón cụt.
Công thức tính diện tích xung quanh hình nón cụt
\(S_{xq} = π(R + r)l\)
trong đó:
Sxq là diện tích xung quanh của hình nón cụt.
l là đường sinh của hình nón cụt.
Công thức tính diện tích toàn phần hình nón cụt
\(S_{tp} = S_xq + S_{đáy lớn} + S_{đáy nhỏ}\)
trong đó:
\(S_{tp}\) là diện tích toàn phần của hình nón cụt.
\(S_{đáy}\) lớn là diện tích đáy lớn của hình nón cụt.
\(S_{đáy}\) nhỏ là diện tích đáy nhỏ của hình nón cụt.
Mối liên hệ giữa đường sinh l và các đại lượng khác
\(l = \sqrt{(h² + (R – r)²}\)
Ứng dụng của hình nón cụt trong toán học
Tính toán thể tích của một chiếc phễu
Giả sử một chiếc phễu có hình dạng nón cụt với chiều cao h = 10cm, bán kính đáy lớn R = 5cm và bán kính đáy nhỏ r = 3cm. Thể tích của chiếc phễu là:
\(V = \frac{1}{3}π * 10 * (5² + 5 * 3 + 3²) = 200π/3 cm³\)
Tính toán diện tích xung quanh của một chiếc mũ
Giả sử một chiếc mũ có hình dạng nón cụt với chiều cao h = 15cm, bán kính đáy lớn R = 10cm và bán kính đáy nhỏ r = 5cm. Diện tích xung quanh của chiếc mũ là:
\(Sxq = π(R + r)l = π(10 + 5) * √(15² + (10 – 5)²) = 250π cm²\)
Giải bài toán hình học
Cho một hình nón cụt có chiều cao h = 12cm, bán kính đáy lớn R = 8cm và bán kính đáy nhỏ r = 4cm. Tính toán đường sinh của hình nón cụt.
Giải:
Đường sinh l của hình nón cụt được tính bằng công thức:
\(l = \sqrt{h² + (R – r)²} = \sqrt{12² + (8 – 4)²} = 12\sqrt{2} cm\)
Bài tập về thể tích hình nón cụt có lời giải
Bài 1: Cho hình nón cụt có chiều cao h = 12cm, bán kính đáy lớn R = 8cm và bán kính đáy nhỏ r = 4cm. Hãy tính thể tích của hình nón cụt.
Lời giải:
Thể tích của hình nón cụt được tính bằng công thức:
\(V = \frac{1}{3}πh(R² + Rr + r²)\)
Thay số vào công thức, ta được:
\(V = \frac{1}{3}π * 12 * (8² + 8 * 4 + 4²) = 448π cm³\)
Bài 2: Một chiếc phễu có hình dạng nón cụt với chiều cao h = 15cm, bán kính đáy lớn R = 6cm và bán kính đáy nhỏ r = 3cm. Hãy tính lượng nước cần thiết để đổ đầy chiếc phễu.
Lời giải:
Lượng nước cần thiết để đổ đầy chiếc phễu chính là thể tích của hình nón cụt.
Thể tích của hình nón cụt được tính bằng công thức:
\(V = \frac{1}{3}πh(R² + Rr + r²)\)
Thay số vào công thức, ta được:
\(V = \frac{1}{3}π * 15 * (6² + 6 * 3 + 3²) = 225π cm³\)
Dạng 2: Tính toán các đại lượng liên quan đến hình nón cụt:
Bài 3: Cho hình nón cụt có thể tích V = 300π cm³, chiều cao h = 10cm và bán kính đáy lớn R = 6cm. Hãy tính bán kính đáy nhỏ r.
Lời giải:
Bán kính đáy nhỏ r được tính bằng công thức:
\(r = \sqrt{\frac{R^2 – \frac{3V}{\pi h}}{}}\)
Thay số vào công thức, ta được:
\(r = \sqrt{6^2 – \frac{3 \times 300\pi}{\pi \times 10}} = 2 \text{ cm}\)
Bài 4: Cho hình nón cụt có thể tích V = 250π cm³ và bán kính đáy lớn R = 5cm. Hãy tính chiều cao h.
Lời giải:
Chiều cao h được tính bằng công thức:
\(h = \frac{3V}{\pi(R^2 + Rr + r^2)}\)
Vì không có thông tin về bán kính đáy nhỏ r, ta không thể tính được giá trị chính xác của h. Tuy nhiên, ta có thể tính được giá trị tối đa của h khi r = 0.
Giá trị tối đa của h được tính bằng công thức:
\(h_{\text{max}} = \frac{3V}{\pi R^2}\)
Thay số vào công thức, ta được:
\(h_{\text{max}} = \frac{3 \times 250\pi}{\pi \times 5^2} = 30 \text{ cm}\)
Bài 5: Tính toán lượng bê tông cần thiết để xây dựng một chiếc cột hình nón cụt có chiều cao h = 8m, bán kính đáy lớn R = 4m và bán kính đáy nhỏ r = 2m.
Lời giải:
Lượng bê tông cần thiết được tính bằng công thức:
\(V = \frac{1}{3}πh(R² + Rr + r²)\)
Thay số vào công thức, ta được:
\(V = \frac{1}{3}π * 8 * (4² + 4 * 2 + 2²) = 80π m³\)
Hình nón cụt có nhiều ứng dụng trong toán học và các lĩnh vực khác. Việc nắm vững công thức tính toán và các ứng dụng của hình nón cụt là điều cần thiết cho học sinh, sinh viên và những người làm việc trong các lĩnh vực liên quan.
Chúc bạn học tốt với toanhoc.edu.vn








